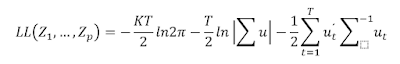Dentro de
las herramientas econométricas que permiten el análisis conjunto de variables
endógenas está el modelo de vectores autorregresivos (VAR), integrando, de
manera implícita, el criterio de simultaneidad entre variables.
En su
forma reducida, un modelo VAR se puede expresar de la siguiente manera:
Donde Yt
es el vector de K variables endógenas, Ai es la matriz KxK de coeficientes del rezago i de las
variables endógenas y εt es el vector de residuos o innovaciones que
siguen un proceso de ruido blanco con media cero y varianza Σ (εt ~N(0,Σ)).
Conforme
a los trabajos de (Keating, 1996) , (Blanchard & Watson, 1987) , (Bernanke, 1986) y (Sims, 1986) ,
quienes desarrollaron una extensión del modelo VAR, introduciendo restricciones
provenientes de la teoría económica conocido como VAR Estructurales (SVAR).
Cuya metodología tiene la ventaja de validar de manera empírica las diferentes
teorías económicas (Carrillo, 2015) .
El
presente trabajo, en su primera parte, utiliza la metodología de (Blanchard & Quah, 1989) para construir el
modelo de largo plazo. De esta manera, el trabajo se constituye en una
variación y adecuación como aporte al modelo presentado por (Carrillo, 2015) [1],
teniendo la siguiente expresión matemática para las variables endógenas:
Donde C
es la matriz de coeficientes de largo plazo de los errores. Cada elemento de la
matriz C es el coeficiente de largo plazo del error de la variable endógena, de
acuerdo con la calibración del modelo. Donde (Blanchard & Quah, 1989) , calibran el modelo
con restricciones teóricas de largo plazo. Sin embargo, para el caso boliviano también
se aplicará restricciones empíricas, conforme a las recomendaciones de (Carrillo, 2015) . En el entendido que
“una macroeconomía realista debe basarse en hechos estilizados, o
generalizaciones empíricas establecidas de forma jerárquica a nivel macro,
sectorial y micro acerca de la economía en estudio” (Kaldor, 1963) .
Respecto
a las generalizaciones empíricas, este trabajo toma como base los trabajos de
investigación de (Gachet, Maldonado, Oliva,
& Ramirez, 2013) . Dichos autores plantean dos pasos para
identificar los hechos estilizados: 1) filtrar el ciclo de las series
económicas a través del filtro de Baxter-King y Hodrick-Prescott en dos etapas[2]; y
2) Identificar las relaciones de las series mediante las correlaciones
cruzadas. Estas relaciones tienen patrones de tiempo y variación (Flores, 2000) .
Por lo
tanto, para imponer las restricciones se utilizará los patrones de tiempo de
las correlaciones. Donde el shock estructural εt , está asociado a
cada variable. Esto nos permite señalar que el shock εcgob , es el
impacto exógeno generado por el consumo de gobierno y así sucesivamente.
ε1t
↔ Consumo de Gobierno[3] (εcgob)
ε2t
↔ Precio Internacional del Petróleo WTI[4] (εind)
ε3t
↔ Inversión[5] (εinv)
ε4t
↔ Importaciones[6] (εm)
ε5t
↔ Consumo de Hogares[7] (εchog)
ε6t
↔ Producto Interno Bruto[8] (εpib)
ε7t
↔ Ingresos por la comercialización de la Producción de Gas Natural[9] (εdir)
ε8t
↔ Exportaciones[10] (εx)
De esta manera, se plantean las restricciones de largo plazo para el modelo, donde todas las variables están sujetas a sus propios shocks; por tanto:
La identificación de los rezagos y parámetros es un
paso esencial para un parsimonioso (Box, Jenkins, & Reinsel, 2008) . Una forma de
selección del número de retardos responde a los criterios de información de
Akaike (AIC), de Hannan-Quin (HQIC) y del bayesiano de Schwarz (SBIC), todos
basados en el Error de Predicción Final (FPE) (Carrillo, 2015) . Cabe destacar que estos modelos utilizan
el determinante de la matriz de covarianza de los errores para un modelo de
orden “p”, el número de parámetros y el tamaño de la muestra. Por tanto,
el valor mínimo de los criterios entre los retardos candidatos es la elección
optima. Según (Lutkepohl, 2005) , los criterios FPE y AIC son
estadísticos convenientes para muestras pequeñas (menores a 100 observaciones)
y para predicciones. Estos criterios son:
En función de lo mencionado, los resultados mostrados en la Figura 9 nos recomiendan utilizar por lo menos 2 rezagos para estimar los coeficientes. Cantidad que satisface las condiciones de estabilidad del modelo, pues no se evidenció ni presencia de auto correlación ni heterocedasticidad en los residuos.
En función de lo mencionado, los resultados mostrados en la Figura 9 nos recomiendan utilizar por lo menos 2 rezagos para estimar los coeficientes. Cantidad que satisface las condiciones de estabilidad del modelo, pues no se evidenció ni presencia de auto correlación ni heterocedasticidad en los residuos.
FIGURA 9: Prueba del Modelo VAR
en su forma reducida, calculado en Stata.
FIGURA 10: Prueba de Condiciones de estabilidad a 2 rezagos. Fuente: Elaboración Propia Stata
FIGURA 10: Prueba de Condiciones de estabilidad a 2 rezagos. Fuente: Elaboración Propia Stata
Después de la identificación del rezago, se obtiene una estimación eficiente de los parámetros, donde las raíces inversas del polinomio AR característico se encuentran del círculo unitario, ver Figura 10. Según
Posteriormente, se maximiza esta expresión para
obtener estimaciones de Z0, . . . ,Zp y de Σu.
En relación de que una de las características de los modelos VAR radica en
presentar coeficientes (Zi) difíciles de interpretar debido a la
naturaleza multivariante. Por lo tanto, se desarrollarán funciones de Impulso Respuesta
(IR) y de Descomposición de la Varianza del Error (FEVD) para superar esta
limitación.
Donde μ = (IK − Z1)−1Z0.
Las distribuciones marginales y conjuntas de los Yt’s, son determinados
únicamente por la distribución de los procesos εt. Aunque a veces,
se asume que un proceso inicia en un periodo específico, también conviene
aceptar que inicia en el pasado infinito (i = −∞).
La representación de medias móviles es una herramienta
especialmente utilizada para examinar la interrelación entre las variables. Los
coeficientes de Zi pueden utilizarse para generar los shocks ε1t
y ε2t en toda la trayectoria del tiempo de x1t y x2t.
Donde la combinación de los elementos zjk de Zi y ut
es conocida como la función de impulso respuesta, los cuales representan a los
multiplicadores de impacto.
Por tanto, es evidente los efectos
expansivos de los principales argumentos económicos en los componentes del PIB
a través de un modelo SVAR de largo plazo. En particular, mediante la función
impulso-repuesta, es posible determinar el impacto de cambios en la variable de
efecto directo (dir) y el consumo de gobierno como gasto público (cgob) sobre
el PIB y su composición. Por otro lado, el modelo nos permite medir la
contribución de las demás variables tomadas en cuenta por el INE, a la
variabilidad del PIB, utilizando la descomposición de la varianza del error.
Sin embargo, respecto a la consideración
de variable de efecto directo (dir), es importante considerar en la actualidad,
que en muchos países del mundo, el mercado de Gas Natural es todavía regulado,
dicha regulación difiere dependiendo del país y por ello hoy en día no existe
un precio de referencia mundial. Sin embargo, experiencias de países como
Estados Unidos, Alemania, Reino Unido, Bélgica, Noruega, Dinamarca, Suecia,
Finlandia, entre otros, el mercado actúa por las fuerzas de la oferta y la
demanda. Por tanto, los precios del Gas Natural son competitivos, y permiten no
sólo la negociación física del activo, sino que además motivan la negociación
de instrumentos financieros derivados, siendo estos considerados mercados
eficientes.
Lo anterior descrito, permite
profundizar más en el análisis de cómo las expectativas que hoy se tiene en
Bolivia sobre el mercado spot de Gas Natural, podría ser un elemento clave a la
hora de evaluar la factibilidad de la implementación de una estrategia de largo
plazo.
Al respecto, debemos considerar que
históricamente las exportaciones de Bolivia del Gas Natural se centran en los
mercados de la Argentina y Brasil.
FIGURA 11: Variación de los precios de exportación de Gas al Brasil. Contrato GSA. Fuente: YPFB
Para el presente trabajo la
variable de efecto directo (dir) que relaciona la producción de Gas Natural y
su incidencia en el PIB, considera el cálculo de los precios de Gas Natural al
Brasil (Contrato GSA), mediante el cual el precio de exportación al Brasil se
fija cada tres meses (Figura 11) y está vinculado a la cotización
de 3 tipos de Fuel Oil, calculado de la siguiente manera (Aguilar &
Valdivia, 2012) :
Cabe hacer notar la incidencia de
los precios internacionales indexados al precio internacional del petróleo,
para nuestro caso WTI, variable de efecto indirecto (ind).
Mientras que la fórmula de fijación
de precios en el contrato de exportación de Gas Natural a la Argentina (Figura
12), es similar a la
estipulada en el Contrato GSA, salvo que se añade a la canasta de 3 tipos de
Fuel Oil, el precio internacional del Diesel Oil, de acuerdo con la siguiente
fórmula (Aguilar & Valdivia, 2012) :
FIGURA 12: Variación de los precios de exportación de Gas Natural a
la Argentina. Fuente: YPFB
Sin embargo, no debemos olvidar que
en la actualidad Bolivia se enfrenta a la firma de un nuevo contrato de compra
y venta de Gas Natural al Brasil por otros 20 años en nuevas condiciones de
reservas, precios y volúmenes.
“El más importante acuerdo
comercial boliviano debe renovarse en 2019. Esto se dará, sin haber certificado
suficientes reservas de gas, tanto para su seguridad energética, como para sus
proyectos de exportación, con una disminución de los precios del barril de
petróleo y con la emergencia de competidores en el mercado regional del GNL” (Orgaz,
2017) .
La estrategia que ya se anuncia por
parte de las empresas transnacionales y Brasil es mantener el tenor del actual
contrato, con el aditamento de más gas a menor precio. Esta estrategia sostiene
que: “Brasil necesita tener las condiciones para ser capaz de renegociar (el
contrato) para que los precios puedan bajar”, según lo expresado por el
ejecutivo de Gas Energy (Tavares, 2014) .
Sin embargo de lo anterior, a
partir de la premisa de (Solow, 1986) : “La producción depende no solo del trabajo y
del capital, sino también de la materia prima disponible en la economía”,
es posible combinar modelos de crecimiento económico con variables ambientales,
tal es el caso de la generación y absorción de residuos contaminantes, y por
ende, relacionar estas variables con aspectos ligados a la Gestión de RSC, así
como indirectamente del Consumo de Gobierno (cgob) y crecimiento del PIB (pib).
En consecuencia, al considerar
variables de protección al Medio Ambiente en el modelo tradicional de
crecimiento económico, el impacto a largo plazo se refleja en la obtención de
un mayor nivel de capital (Ibarra, 2012) . Ver los escenarios de crecimiento en
la Figura 13.
FIGURA 13: Escenarios de crecimiento. Fuente: Elaboración propia.
La incorporación de la materia
prima en el modelo clásico[11]:
,
permite establecer límites a la función de producción:
La incorporación de variables
ecologistas y de RSC, modifica ligeramente el sistema de ecuaciones
diferenciales, y busca una solución al determinar los valores característicos del Jacobiano.
[1] Se
cuenta con la autorización de Paul Carrillo Maldonado para el uso de su rutina
en Stata. Paul Carrillo es Ingeniero en Ciencias Económicas y Financieras de la
Escuela Politécnica Nacional (EPN) y Licenciado de la Universidad Jean Monnet
(convenio con la EPN). Cuenta con una Maestría en Economía con mención en
Economía del Desarrollo (FLACSO). PhD en Economía del Desarrollo en el Programa
Doctoral de FLACSO. Trabajó en el Banco Central del Ecuador, el Servicio de
Rentas Internas y el Ministerio de Economía como Coordinador de Política
Económica. Ha publicado artículos en revistas académicas nacionales e
internacionales.
[2] Se
utilizará el filtro de Baxter-King, debido a que este permite una construcción
de medias móviles que separa los componentes periódicos de una serie de tiempo
que está en una banda específica de frecuencias, sin tomar valores de manera
discrecional para encontrar las relaciones empíricas, lo que permite una mayor consistencia
que el presentado por el modelo de Hodrick-Prescott.
[3] cgob
= Consumo de Gobierno. Cuenta INE: Gasto de consumo final de la administración
pública (En miles de bolivianos de 1990)
[4] Ind
= Variable de efecto Indirecto. Precio Internacional del Petróleo WTI (Fuente:
FRED Economic Data). Expresado en US$ por Barril.
[5] inv
= Inversión. Cuenta INE: Formación bruta de capital fijo (En miles de
bolivianos de 1990)
[6] m
= Importaciones. Cuenta INE: Importaciones de bienes y servicios (En miles de
bolivianos de 1990)
[7] chog
= Consumo de Hogares. Cuenta INE: Gasto de consumo final de los hogares e IPSFL
(En miles de bolivianos de 1990)
[8] pib
= Producto Interno Bruto. Cuenta INE: Bolivia: Producto Interno Bruto por
semestre, según tipo de gasto (En miles de bolivianos de 1990)
[9] dir
= Variable de efecto Directo. Cuenta INE: Petróleo Crudo & Gas Natural (En
miles de bolivianos de 1990). Contrastado con los Ingresos por la
comercialización de la Producción de Gas Natural, calculado a partir de la
producción en los campos de producción (Contratos GSA: Brasil y Argentina)
(Fuente: YPFB, MH, ANH), precio internacional Henry Hub, derivados de petróleo
(Fuente: FRED Economic Data), tipo de cambio (Fuente: INE). Dicha variable
tiene un comportamiento de tipo estacional debido a que se correlaciona de
manera directa con la demanda de Gas Natural, por parte de Brasil y Argentina,
quienes demandan mayores volúmenes en épocas de invierno, aunque el contrato
establece una forma “Take or Pay”.
[10] x =
Exportaciones. Cuenta INE: Exportaciones de bienes y servicios (En miles de
bolivianos de 1990)
[11] Y= Producto total
de la economía; L= Factor trabajo de la economía; K= Capital utilizado en la
economía, MP=Materia Prima